
有多少同学打算在今年5月份把爱德思的纯数P1-P4一次性考完?在P1到P4中都有微积分的知识,许多同学学到后面会觉得有点思维混乱。
那么这里我们梳理一下不同分册这样划分微积分知识的原因,并通过真题举例说明核心考点。本期是P1的核心内容梳理。
P1:初识微积分——千呼万唤始出来,犹抱琵琶半遮面
核心概念:直线斜率,多项式,积分套公式。

解说:P1的微积分实际上很难说有多少微积分的思想,并没有强调微积分中重要的极限,变化与累积的概念。如果说确实说明了什么核心概念,那可能也就是“积分是微分的逆运算”这一原理了。实际上P1的题目要拿分很容易,抓住两个重点,第一就是最简单的多项式积分与微分的公式,第二就是要了解对一个函数进行微分,得到的是函数在某一点的切线斜率计算的“算式”。
核心知识点1: 微分和积分的公式,二阶导数
注意各种不同指数形式的变化,例如就是,就是。这种变化在微分和积分公式运算的时候都经常考。
核心知识点2:切线与法线(Tangent 和 Normals)
要注意看题目让你求的到底是切线还是法线,切线和法线的斜率相乘等于,每年都有同学因为没看清题目到底问的是切线还是法线而求错了直线,在对答案的时候破防。
核心知识点3:简单函数的最值
因为求导之后能够得到切线,而多项式函数,比如二次或者三次函数,再取最大值或者最小值的时候,切线是和轴平行的,也就是说斜率(slope),因此一阶导数在这个地方也是。这一点是很重要的一点,对我们研究函数的表现很有帮助,但相关的知识点要在P2才会继续考察。
总的来说,如果同学们学过IG附加数的微积分的话,学习A-level并不困难,而对于体制内进入国际高中体系没有学过微积分的同学来说,这里接触的难度也并不大。
例题与总结:
1 简单题:纯计算
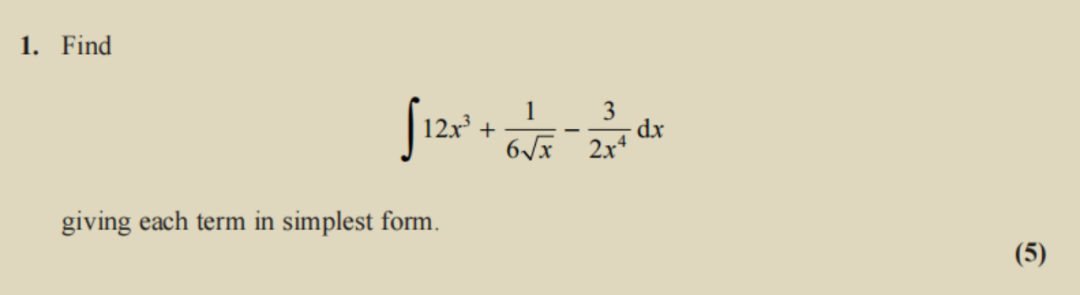
这个是2022年的一道简单题,不需要你对微积分有任何本质性的理解,只要你会背上面的积分公式就行了。需要注意最后不要忘了加上常数项C。
考察的难点就在于不同形式的幂函数的转化,这里出现了和,同学们需要知道对应的应该取几。
答案:

2 难题1:多次求导带参数 主要考察运算

因为P1积分学的实在是简单,所以P1难题这边还是倾向于在求导方面出题。但是这道题通过原函数,一阶导数和二阶导数之间的关系全面的考察到了积分和微分的全部知识点。这也是前面提到的P1中几乎是“唯一”包含的微积分原理:积分是微分的逆运算。
因此第一问直接对给出的一阶导数求导得到二阶导数,代入题目中给的点的数据即可。第二问则是在第一问的基础上对一阶导数的表达式进行积分,和之前的题目一样,同样都是套公式。
最后要注意,积分完了之后要有常数项C,用题目给出的曲线经过的点的坐标信息就可以解出C的值。



3 难题2:切线与法线 (Tangent 和 Normals)
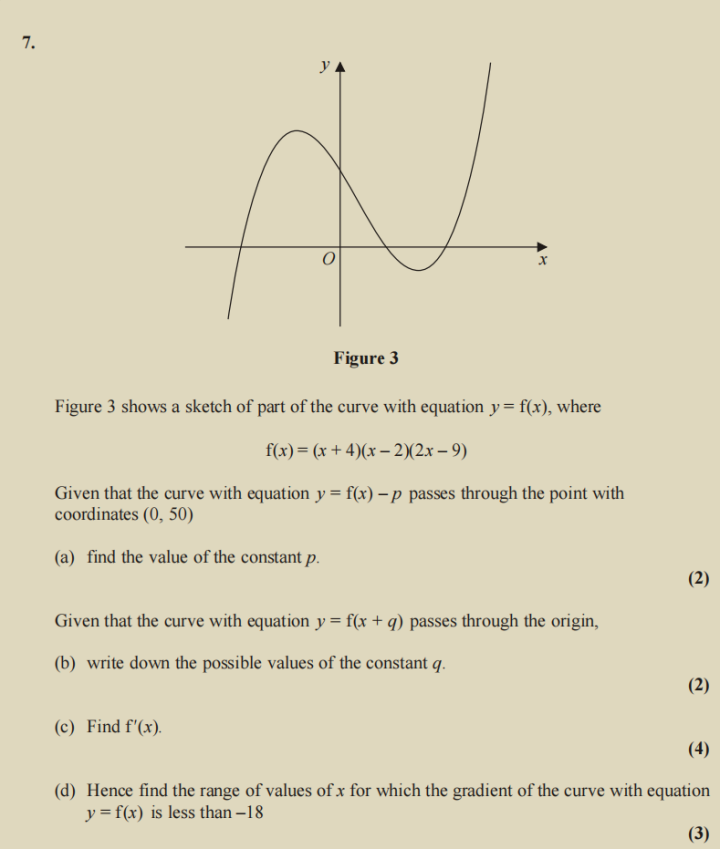
这道题第一问和第二问都比较简单,只要能够理解函数和函数经过的点的关系就能解出p。第三问同学要大胆的拆掉括号然后在进行求导,因为在这里你还没有学过不同的式子相乘之后要怎么求导。所以看到括号就大胆的拆就可以了。
最后一问需要同学们理解,c问计算出来的的表达式实际上就是切线斜率(gradient of the curve),因此最后一问实际上变成了二次函数不等式的求解。看起来是在考察微积分,实际上真正的计算和微积分没有什么关系。只要解出了二次方程就可以了。

希望以上的内容对于同学们准备爱德思数学P1微积分部分的考试有所帮助~
历年真题+测试题大合集超详细
长按图片即可添加客服



